What Best Describes an Irrational Number

By Ra_Kathryn235 11 May, 2022 Post a Comment

Any real number that cannot be written as a fraction. Any real number that is not rational.

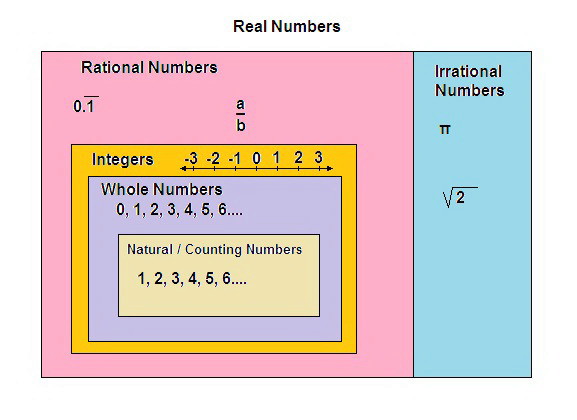
Rational And Irrational Numbers Explained With Examples And Non Examples And Pictures

So z will always be irrational number.

. D- A number that cannot be expressed as a fraction where p and q are integers. A number that cannot be written as the ratio of two integers. We arent saying its crazy.

Which description best describes an irrational number. And also it can not be expressed as terminating decimal or repeating decimal. Irrational means no ratio so it isnt a rational number.

An irrational number is simply a number that cannot be written as a fraction. It comes from the the word ratio. 1- a number with a nonterminating decimal expansion 2- a number with a nonrepeating decimal expansion 3- a.

Product of two Irrational Numbers. The number pi and square roots of non-perfect squares are examples of. Irrational numbers are numbers with non-repeating and non-terminating decimal expansion.

Up to 10 cash back An irrational number is any number that cannot be written as a fraction of whole numbers. - non repeating. Now let us elaborate irrational numbers could be written in decimals but not in the form of fractions which means.

An irrational number is. A real number that can NOT be made by dividing two integers an integer has no fractional part. 15 is rational but π is irrational Irrational means not Rational no ratio.

Find the area of the square with side. Terms in this set 18 rational number. If N is irrational then N is not equal to pq where p.

Learn about the definition of irrational numbers and discover. They have an infinite non-repeating sequence of numbers after the decimal point. In mathematics the word has a completely different meaning.

Irrational numbers are real numbers that cannot be expressed as a ratio of two integers or as simple fractions. Imara used these steps to find the length of the hypotenuse of the right triangleStep 1. - not a perfect square.

In decimal form all irrational numbers are nonterminating and nonrepeating perfect square a number whose square root is rational. Tap card to see definition. An Irrational Number is a real number that cannot be written as a simple fraction.

A number that cannot be approximated by a decimal. An irrational number is a type of real number which cannot be represented as a simple fraction. An irrational number can not be expressed as a fraction or ratio of integers like where p and q are integers.

This is a contradiction which means that the previous assumption was wrong. It cannot be expressed in the form of a ratio. A non-repeating non-terminating decimal.

Click card to see definition. A ratio nal number is one that can be written as the ratio of two integers. An irrational number cannot be expressed as a ratio between two numbers and it cannot be written as a simple fraction because there is not a finite number of numbers when written as a.

The numbers which are not rational numbers are called irrational numbers. Check out the definition learn an important property of these special numbers and take a look at some. Irrational and Rational Numbers.

Which of the following must describe an irrational number. Find the area of the square with side lengths of 20.

Classifying Numbers Review Article Khan Academy